摘要： 你是否背过“通解 = 特解 + 齐次通解”这个公式？但你真的理解它背后的几何图景吗？今天，我们深入“零空间”，揭开线性方程组解集的真实面纱。
0. 一个奇怪的公式
前情回顾:在上一期中,我们学习了如何从"列图像"的角度理解线性方程组,把 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 看作向量的线性组合问题。
在解非齐次线性方程组 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 时，老师总会让我们先解对应的齐次方程组 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$。 最后给出的通解公式是： $$ \boldsymbol{x} = \boldsymbol{x}_p + \boldsymbol{x}_h $$
- $\boldsymbol{x}_p$ 是 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 的一个特解 (Particular Solution)。
- $\boldsymbol{x}_h$ 是 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$ 的齐次通解 (Homogeneous Solution)。
很多同学对此感到困惑：我明明求的是 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 的解，为什么要费劲去求 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$？那个 $0$ 到底有什么魔力？
今天，我们就用几何的视角，把这个公式“画”出来。
1. 齐次方程：寻找“零空间”
首先，我们来看看 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$。 $$ \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$ 显然，$(0,0)$ 肯定是一个解。除此之外呢？ 你会发现，所有满足 $x + 2y = 0$ 的向量都是解，比如 $(-2, 1), (-4, 2)$ 等等。
这些解构成了一条通过原点的直线。 在数学上，我们给它起了一个很酷的名字：核空间 (Kernel) 或 零空间 (Null Space)。
为什么它很重要？
因为零空间是一个“子空间” (Subspace)。 这意味着它具有完美的代数性质：
- 封闭性：你在零空间里怎么加、怎么乘，结果还在零空间里。
- 过原点：它一定包含零向量。
你可以把它想象成一个过原点的平坦结构（直线、平面、或高维平面）。
2. 非齐次方程：平移的艺术
现在，我们回到 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$。 $$ \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 3 \\ 6 \end{bmatrix} $$ 我们很容易找到一个特解，比如 $\boldsymbol{x}_p = (1, 1)$。 那么，其他的解在哪里呢？
神奇的事情发生了：所有的解，其实就是把那个“零空间”整体平移了一下！
想象一下：
- 零空间是一条过原点的直线 $L_0$。
- 特解 $\boldsymbol{x}_p$ 是一个向量，把原点“推”到了 $(1,1)$ 的位置。
- 解集 就是被推开后的那条直线 $L$。
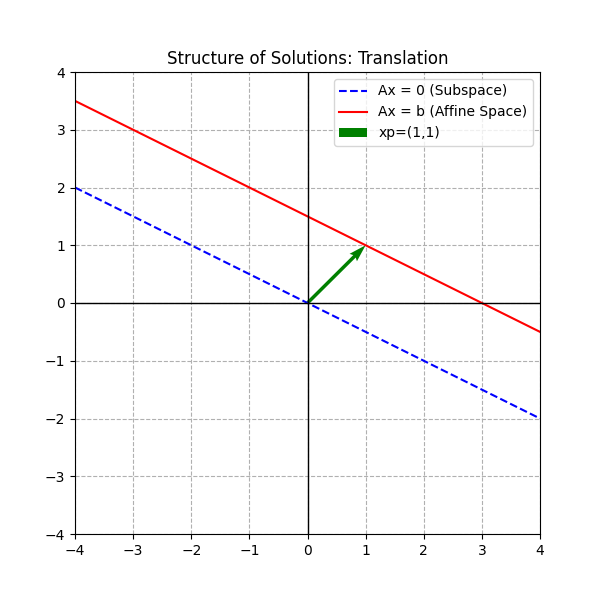(图注：齐次解（蓝色虚线）过原点，非齐次解（红色实线）是它的平移)
这就是公式 $\boldsymbol{x} = \boldsymbol{x}_p + \boldsymbol{x}_h$ 的几何含义：
非齐次解集 = 特解向量 + 零空间
3. 仿射空间：失去“原点”的悲伤
这里有一个非常重要的概念陷阱。 虽然非齐次方程的解集看起来也是一条直线（或平面），但它不是线性子空间。
为什么？ 因为它不过原点！ 在数学上，我们称之为仿射空间 (Affine Space)。
- 子空间 (Subspace)：必须过原点，结构完美，像是一个“家”。
- 仿射空间 (Affine Space)：是被平移后的子空间，虽然形状一样，但失去了“零点”这个根基。
这就像：
- 齐次解是“过起点的跑道”。
- 非齐次解是“起跑线前移了 10 米的跑道”。
4. 总结
为什么我们要先解 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$？ 因为 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$ 刻画了解集的形状（是直线？平面？还是点？）。 而 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 只是决定了解集的位置（平移到了哪里）。
- $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$ (齐次)：决定了方向和维度（Kernel）。
- $\boldsymbol{b}$ (非齐次项)：决定了位移。
当你理解了这一点，那个枯燥的通解公式 $\boldsymbol{x} = \boldsymbol{x}_p + \boldsymbol{x}_h$，是不是瞬间变得生动起来了？它描述的不是一串数字，而是一次空间的平移变换。
下一期，我们将站得更高，把矩阵看作一台机器，从线性变换的角度，彻底打通 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 的任督二脉。
下一期预告：线性方程组专题(3)：上帝视角——矩阵是一台"降维打击"的机器
互动思考： 如果 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$ 只有零解（零空间只有原点），那么 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 的解会是什么样子的？（提示：形状是什么？位置在哪里？）