摘要： 为什么 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 难住了 90%的初学者？因为你还在用高中的“几何直觉”硬套大学的“线性思维”。今天，我们拆掉思维里的墙，从“行”走到“列”，带你领略线性代数真正的威力。
0. 一个被忽视的“常识”
在数学的广袤宇宙中，几乎所有的问题最终都会汇聚成一个形式： $$ \mathbf{A}\boldsymbol{x} = \boldsymbol{b} $$ 其中，$\mathbf{A}$ 是矩阵，$\boldsymbol{x}$ 是未知数，$\boldsymbol{b}$ 是目标。
对于这个方程，你一定不陌生。回想一下高中，当我们面对一个二元一次方程组：
$$ \begin{cases} x + y = 2 \\ x - y = 0 \end{cases} $$
你的脑海里浮现出的画面是什么？
我敢打赌，绝大多数人的第一反应是：画两条直线，找它们的交点。
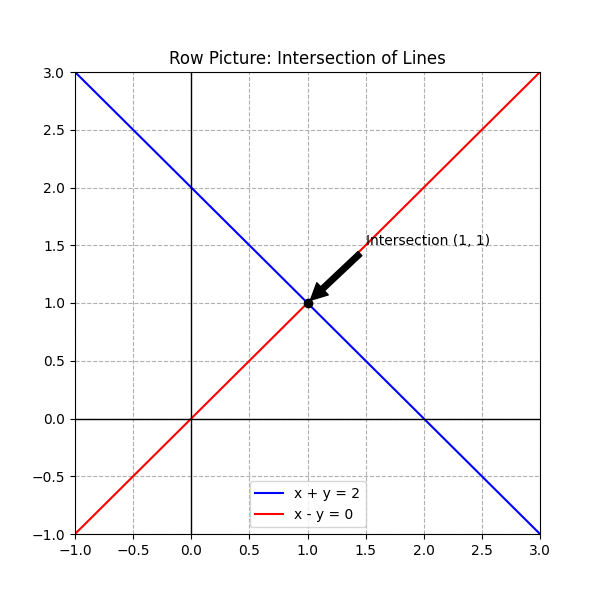(图注：这是我们熟悉的“行图像”)
没错，这很直观，很正确。但在线性代数的世界里，这种视角（我们称为行图像 (The Row Picture)）虽然经典，却往往会限制你的想象力。当你面对 100 个变量、100 个方程时，你还能想象 100 维空间里的 100 个超平面相交吗？
今天，我要邀请你换一副眼镜，从列图像 (Column Picture) 的角度重新审视它。这不仅是视角的转换，更是从“算术”到“代数”的思维跃迁。
1. 什么是“行图像”？（复习一下）
所谓“行图像 (The Row Picture)”，就是把方程组看作是多个几何图形的交集。
- 2 维时：是直线的交点。
- 3 维时：是平面的交线/交点。
- n 维时：是 $n-1$ 维超平面 (Hyperplane) 的交集。
它的本质是做减法。 全空间 $\mathbb{R}^n$ 本来是无限自由的。每增加一个方程（也就是矩阵的一行），就相当于引入了一个约束，对空间进行一次“切割”。
- 切一刀，维数减一。
- 再切一刀，维数再减一。
- 切到最后，剩下的那个点（如果存在的话），就是解。
这种视角对于理解“约束”很有用，但对于理解“结构”却显得力不从心。
2. 颠覆认知的“列图像”
现在，让我们施展魔法，把方程组 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 拆开来看。
$$ \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} $$
我们不再横着看（行），而是竖着看（列）。 我们将矩阵 $\mathbf{A}$ 拆分为两个列向量：$\boldsymbol{c}_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 和 $\boldsymbol{c}_2 = \begin{bmatrix} 1 \\ -1 \end{bmatrix}$。
此时，方程组奇迹般地变成了一个向量的线性组合问题：
$$ x \begin{bmatrix} 1 \\ 1 \end{bmatrix} + y \begin{bmatrix} 1 \\ -1 \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \end{bmatrix} $$
这里的几何意义完全变了！
现在，问题不再是“寻找交点”，而是变成了：
我手头有两个积木（向量 $\boldsymbol{c}_1$ 和 $\boldsymbol{c}_2$），我该如何通过伸缩（乘以 $x, y$）和叠加（加法），拼出目标积木（向量 $\boldsymbol{b}$）？
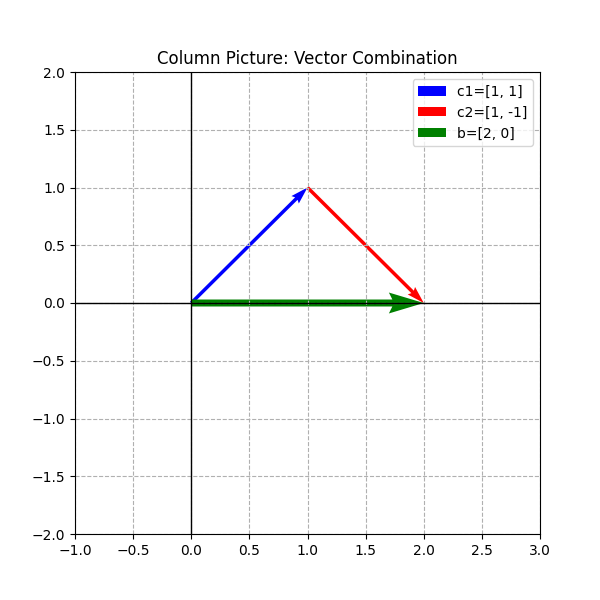(图注：列图像——向量的合成)
在这个例子中，答案是显而易见的： 取 1 个 $\boldsymbol{c}_1$（$x=1$），再取 1 个 $\boldsymbol{c}_2$（$y=1$），它们首尾相接，刚好走到点 $(2,0)$ 的位置。 所以解是 $x=1, y=1$。
3. 为什么要费劲学“列图像”？
你可能会说：“原来的方法也能算出答案啊，为什么要折腾？”
问得好。但在更高维度的世界里，“列图像”才是王道。它引出了线性代数中最重要的概念之一：列空间 (Column Space)。
试想，如果 $\boldsymbol{b}$ 变了，变成了 $\begin{bmatrix} 3 \\ 5 \end{bmatrix}$，或者其他任何向量。 我们真正关心的是：这两个列向量，到底能拼出多少种可能性？
- 它们能铺满整个二维平面吗？（在这个例子里，能！）
- 如果 $\boldsymbol{c}_1$ 和 $\boldsymbol{c}_2$ 共线了（比如 $\boldsymbol{c}_2$ 也是 $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$），它们还能铺满平面吗？（不能，只能铺满一条线！）
这就是线性相关性的几何直观。
- 如果列向量是“独立”的，它们就能张成一个更大的空间。
- 如果列向量是“冗余”的（线性相关），它们张成的空间就会坍缩。
维度的反转
细心的你可能发现了：
- 在行图像里，增加未知数 ($n$) 会增加空间的维数；增加方程 ($m$) 是在增加约束（多切一刀）。
- 在列图像里，增加未知数 ($n$) 是在增加“积木”的数量；增加方程 ($m$) 则是让向量“变长”了，也就是向量所在空间的维数增加了。
这就是为什么在处理大数据（$m$ 很大）时，列图像往往更能帮我们理解数据的“形状”。
4. 总结
- 行图像关注的是约束与交集（切蛋糕）。
- 列图像关注的是生成与张成（搭积木）。
当你开始习惯用“列”的眼光看矩阵，你会发现，矩阵不再是一堆枯燥的数字，而是一组充满生命力的向量，它们在空间中伸展、叠加，构建出丰富多彩的几何结构。
下一期，我们将深入探讨：当积木搭不成目标形状时会发生什么？ 也就是 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 无解或有无穷多解背后的秘密——零空间与仿射空间。
下一期预告：线性方程组专题(2)：解的形状——为什么"齐次"那么重要？
互动思考： 你能画出 $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}$ 的列图像吗？在评论区告诉我你的理解！