摘要： 如果说“列图像”是搭积木，“解的结构”是空间平移，那么今天我们要站在上帝视角，把矩阵看作一台精密的“空间变换机器”。这将是你理解线性代数最关键的一次思维升华。
0. 矩阵的真面目
系列回顾：专题(1) 行与列图像 | 专题(2) 解的结构
在之前的文章里，我们把矩阵 $\mathbf{A}$ 看作是一组方程的系数（行视角），或者是一组积木的集合（列视角）。 但现代数学家更喜欢把它看作一个函数，或者说一个映射 (Mapping)。
$$ T(\boldsymbol{x}) = \mathbf{A}\boldsymbol{x} $$
把 $\mathbf{A}$ 想象成一台机器：
- 输入：一个向量 $\boldsymbol{x}$（来自 $\mathbb{R}^n$ 空间）。
- 处理：经过矩阵 $\mathbf{A}$ 的乘法运算。
- 输出：一个新的向量 $\boldsymbol{b}$（进入 $\mathbb{R}^m$ 空间）。
这不仅仅是数字的计算，而是空间的变换。
- 它可以把一个正方形拉伸成平行四边形。
- 它可以把整个空间旋转、镜像。
- 它甚至可以把高维空间“压扁”成低维空间。
1. 核空间：被“吃掉”的维度
还记得我们在上一期讲的核空间 (Kernel) 吗？也就是 $\mathbf{A}\boldsymbol{x}=\boldsymbol{0}$ 的解集。 在“机器”的视角下，它的含义变得有点可怕：
核空间里的所有向量，在经过机器 $\mathbf{A}$ 处理后，都变成了 $\boldsymbol{0}$。
换句话说，这些向量所代表的信息，被这台机器毁灭了，压缩了，降维了。
- 如果 $\text{Ker}(\mathbf{A})$ 只有零向量：说明机器保留了所有信息，没有“压扁”任何维度。变换是可逆的。
- 如果 $\text{Ker}(\mathbf{A})$ 是一条直线或平面：说明机器把整个空间沿着这个方向“拍扁”了。
这就是为什么方阵如果行列式为 0（奇异），它就不可逆。因为它把一部分空间“压”没了，你再也回不去了。
2. 像空间：机器的“能力边界”
机器输出的所有可能的向量 $\boldsymbol{b}$ 的集合，构成了另一个空间。 我们称之为像空间 (Image Space)，其实它就是我们第一期讲的列空间 (Column Space)。
$$ \text{Im}(\mathbf{A}) = C(\mathbf{A}) $$
这代表了这台机器的能力边界。
- 无论你怎么调整输入 $\boldsymbol{x}$，输出 $\boldsymbol{b}$ 永远跑不出这个空间。
- 如果 $\boldsymbol{b}$ 在像空间里，方程有解。
- 如果 $\boldsymbol{b}$ 在像空间外，方程无解（机器造不出这个产品）。
3. 秩-零化度定理：能量守恒
在线性代数中，有一个堪称“能量守恒定律”的伟大定理：秩-零化度定理 (Rank-Nullity Theorem)。
$$ n = \text{rank}(\mathbf{A}) + \text{nullity}(\mathbf{A}) $$
- $n$：输入的总维度（原本的自由度）。
- $\text{rank}(\mathbf{A})$：像空间的维度（输出的有效维度）。
- $\text{nullity}(\mathbf{A})$：核空间的维度（被压扁的维度）。
直观理解： 你原本有 $n$ 维的信息。经过机器 $\mathbf{A}$ 处理后： 一部分维度保留了下来，变成了秩 (Rank)； 另一部分维度被压缩成了 0，变成了零化度 (Nullity)。 它们加起来，必须等于原本的总维度 $n$。
4. 终极图景：四个基本子空间
至此，我们终于拼完了线性代数的完整拼图。 对于任意矩阵 $\mathbf{A}$，宇宙中存在四个神圣的子空间：
- 列空间 (Column Space)：机器能造出的所有产品。
- 零空间 (Null Space)：被机器毁灭的所有原料。
- 行空间 (Row Space)：机器真正利用的有效原料（与零空间正交）。
- 左零空间 (Left Null Space)：机器造不出的产品所在的“死角”。
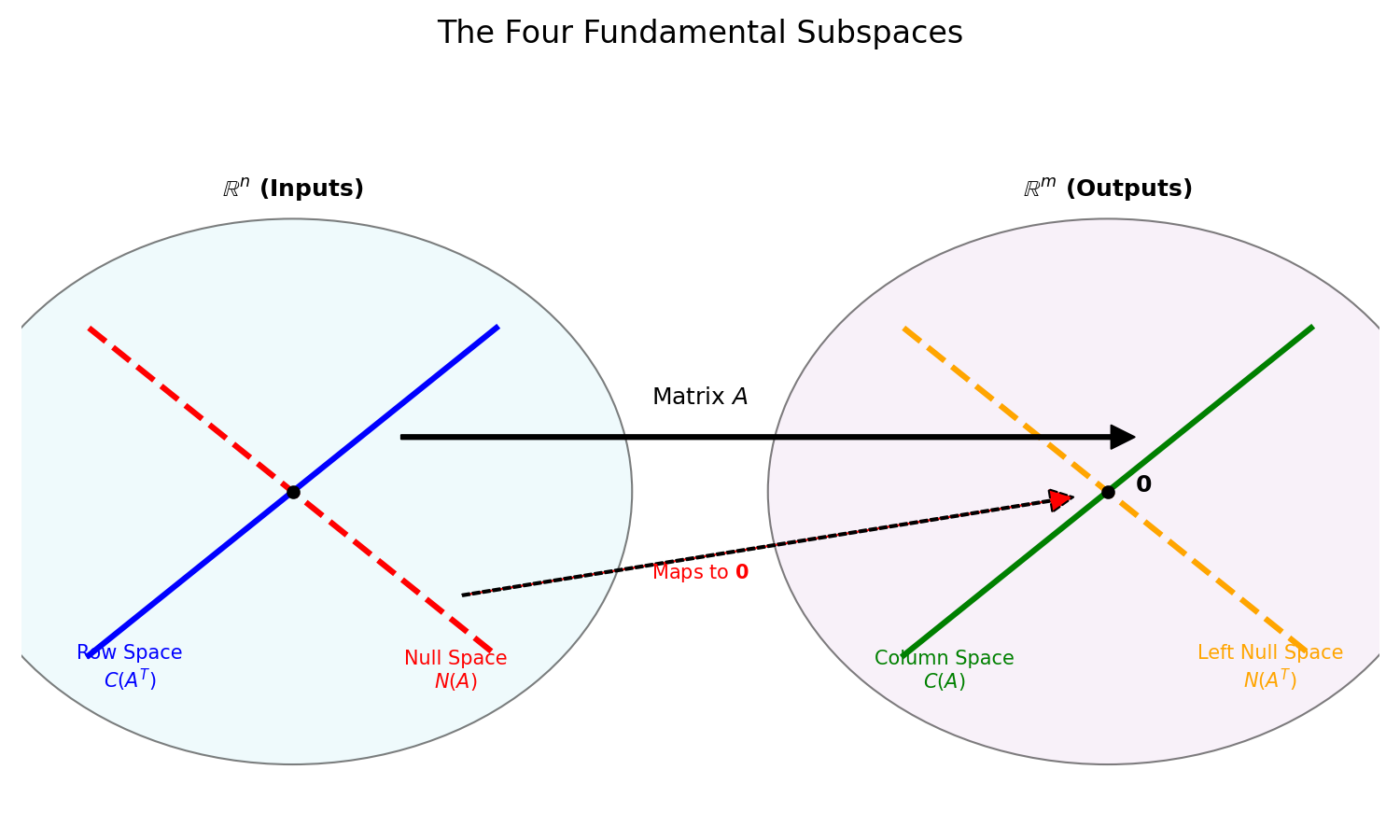(图注：Strang 教授经典的“四个子空间”图示，展示了矩阵变换的完整几何图景)
当你能闭上眼睛，在脑海中看到这四个空间如何正交、互补、映射时，恭喜你，你已经掌握了线性代数的心脏。
5. 图解核心：为什么行空间指向列空间？
你可能注意到了图中那个连接“行空间”和“列空间”的箭头。这其实揭示了矩阵变换最精妙的性质。
对于任意向量 $\boldsymbol{x}$，我们都可以把它分解为两部分：$\boldsymbol{x} = \boldsymbol{x}_r + \boldsymbol{x}_n$。
- $\boldsymbol{x}_n$ 属于零空间（会被矩阵变成 $\boldsymbol{0}$）。
- $\boldsymbol{x}_r$ 属于行空间（与零空间垂直）。
当我们进行矩阵乘法时： $$ \mathbf{A}\boldsymbol{x} = \mathbf{A}(\boldsymbol{x}_r + \boldsymbol{x}_n) = \mathbf{A}\boldsymbol{x}_r + \mathbf{0} = \mathbf{A}\boldsymbol{x}_r $$
这意味着：输出向量 $\boldsymbol{b}$ 完全是由 $\boldsymbol{x}$ 中的行空间分量 $\boldsymbol{x}_r$ 决定的！
更重要的是，在这个限制下，矩阵 $\mathbf{A}$ 变成了一个**一一对应（可逆）**的映射：
行空间里的每一个向量，都完美地对应着列空间里的一个向量。
这就是为什么我们说矩阵 $\mathbf{A}$ 是连接这两个空间的桥梁。
结语： 从 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 出发，我们一路走过了：
- 行图像的超平面交集；
- 列图像的向量积木；
- 解结构的空间平移；
- 线性变换的降维打击。
希望这三篇文章，能帮你把那些枯燥的公式，变成脑海中生动的几何动画。线性代数不难，它只是需要一点想象力。