引言

在 矩阵对角化那些事 里，我们把对角阵捧上了天——所有的基向量各司其职，互不干扰，这是矩阵最理想的“完全体”。

但现实往往不那么完美。当特征向量“不够用”时（几何重数 < 代数重数），矩阵就没法变成漂亮的对角阵。这就像你手里的积木不够搭出完美的城堡。

这时候，我们不能直接摆烂，而是要寻找一种 “妥协的艺术” —— 既然做不到完全独立，那能不能让它们尽量少一点纠缠？

这份妥协的产物，就是 Jordan 标准形。

灵魂拷问：如何计算“几乎对角”矩阵的幂？

引子例题 计算 Jordan 块 $\mathbf{J} = \begin{pmatrix} \lambda & 1 \\ 0 & \lambda \end{pmatrix}$ 的 $n$ 次幂 $\mathbf{J}^n$。

【直觉破局】

硬算会很痛苦，但如果你换个角度看它： $$ \mathbf{J} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda \end{pmatrix} + \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} = \lambda \mathbf{E} + \mathbf{N} $$ 把它拆成“纯缩放” $\lambda \mathbf{E}$ 和“纯位移” $\mathbf{N}$。注意，这个 $\mathbf{N}$ 是个狠角色——幂零矩阵（Nilpotent Matrix），它走两步就归零了（$\mathbf{N}^2 = \mathbf{O}$）。

利用二项式定理（因为 $\lambda \mathbf{E}$ 和 $\mathbf{N}$ 可交换）： $$ (\lambda \mathbf{E} + \mathbf{N})^n = C_n^0 (\lambda \mathbf{E})^n + C_n^1 (\lambda \mathbf{E})^{n-1} \mathbf{N} + \underbrace{C_n^2 (\lambda \mathbf{E})^{n-2} \mathbf{N}^2 + \dots}_{\text{全被 } \mathbf{N}^2 \text{ 杀死了}} $$ 一切瞬间清爽： $$ \mathbf{J}^n = \lambda^n \mathbf{E} + n \lambda^{n-1} \mathbf{N} = \begin{pmatrix} \lambda^n & n\lambda^{n-1} \\ 0 & \lambda^n \end{pmatrix} $$

直觉： Jordan 块 = “静止的主旋律” ($\lambda \mathbf{E}$) + “微小的杂音” ($\mathbf{N}$)。

核心重构：广义特征向量的链条

1. 几何直觉：幂零矩阵与多米诺骨牌

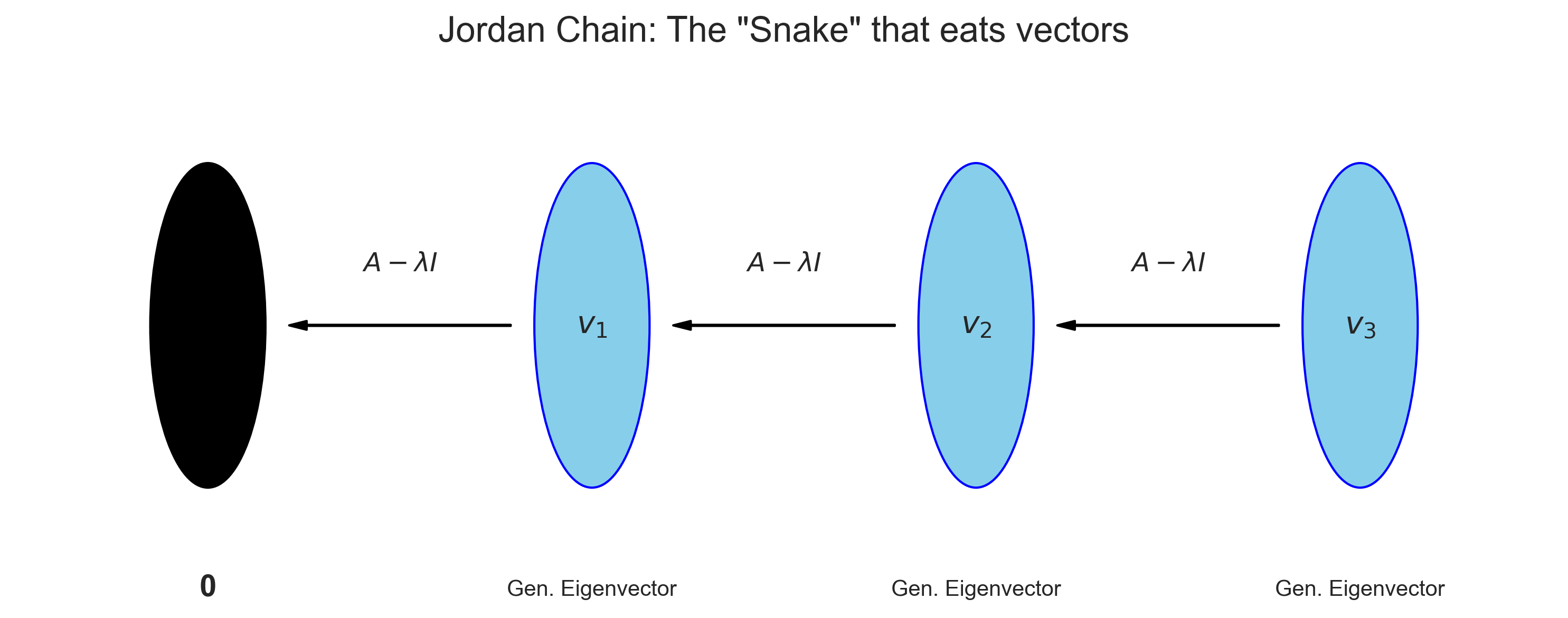◎ Jordan 链示意图：向量被逐级传递

那个捣乱的 $\mathbf{N} = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}$ 到底干了什么？

• 它把 $\boldsymbol{e}_3$ 降维打击成 $\boldsymbol{e}_2$。
• 把 $\boldsymbol{e}_2$ 降维打击成 $\boldsymbol{e}_1$。
• 最后把 $\boldsymbol{e}_1$ 直接推入虚无，变成 $\mathbf{0}$。

这就不难理解为什么它没法对角化了——基向量之间不再是平等的，而是形成了一副 “多米诺骨牌”（Jordan Chain）： $$ \boldsymbol{v}_3 \xrightarrow{\mathbf{A}-\lambda \mathbf{E}} \boldsymbol{v}_2 \xrightarrow{\mathbf{A}-\lambda \mathbf{E}} \boldsymbol{v}_1 \xrightarrow{\mathbf{A}-\lambda \mathbf{E}} \mathbf{0} $$

2. 数学推导：链条的由来

假设有一个 3 阶 Jordan 块 $\mathbf{J} = \begin{pmatrix} \lambda & 1 & 0 \\ 0 & \lambda & 1 \\ 0 & 0 & \lambda \end{pmatrix}$。 我们想找一组基 $\mathbf{P} = (\boldsymbol{v}_1, \boldsymbol{v}_2, \boldsymbol{v}_3)$ 把它变出来，即 $\mathbf{A}\mathbf{P} = \mathbf{P}\mathbf{J}$。

把矩阵乘法展开看，秘密就藏在列向量的递推关系里：

1. 第一列：$\mathbf{A}\boldsymbol{v}_1 = \lambda \boldsymbol{v}_1$

   • $\implies (\mathbf{A} - \lambda \mathbf{E})\boldsymbol{v}_1 = \mathbf{0}$
   • 解读：$\boldsymbol{v}_1$ 是正儿八经的特征向量，链条的尽头。

2. 第二列：$\mathbf{A}\boldsymbol{v}_2 = 1\cdot\boldsymbol{v}_1 + \lambda \boldsymbol{v}_2$

   • $\implies (\mathbf{A} - \lambda \mathbf{E})\boldsymbol{v}_2 = \boldsymbol{v}_1$
   • 解读：$\boldsymbol{v}_2$ 被变换后，“溢出”了一点 $\boldsymbol{v}_1$。它是广义特征向量。

3. 第三列：$\mathbf{A}\boldsymbol{v}_3 = 1\cdot\boldsymbol{v}_2 + \lambda \boldsymbol{v}_3$

   • $\implies (\mathbf{A} - \lambda \mathbf{E})\boldsymbol{v}_3 = \boldsymbol{v}_2$
   • 解读：$\boldsymbol{v}_3$ 接着“溢出” $\boldsymbol{v}_2$。

总结： 这一组向量 {$\boldsymbol{v}_1, \boldsymbol{v}_2, \boldsymbol{v}_3$} 就构成了一条紧密的链条。

想象一个救火传递（Bucket Brigade）：$\boldsymbol{v}_3$ 手里的水（信息）传给了 $\boldsymbol{v}_2$，$\boldsymbol{v}_2$ 传给了 $\boldsymbol{v}_1$，最后 $\boldsymbol{v}_1$ 把水泼向了火场（零向量）。

• 链头 ($\boldsymbol{e}$ 向量)：即 $\boldsymbol{v}_1$，真正的特征向量。链头的数量 = 几何重数（有多少条链）。
• 链身 ($\boldsymbol{v}$ 向量)：即 $\boldsymbol{v}_2, \boldsymbol{v}_3$，广义特征向量。它们凑够了代数重数（链条的总长度）。
• 粉碎机 ($\mathbf{A}-\lambda \mathbf{E}$)：沿着链条把向量逐级“推倒”，直到归零。

3. 最小多项式：一眼看穿链条长度

特征多项式 $f(\lambda)$ 告诉我们有哪些链条（特征值），而最小多项式 $m(\lambda)$ 则暴露了最长的那条链有多长。

• 核心判据： 矩阵 $\mathbf{A}$ 可对角化 $\iff$ 最小多项式没有重根（所有链条长度都为 1）。
• 举例：
  • $m(\lambda) = (\lambda-1)(\lambda-2) \implies$ 大家都是单节点链 $\implies$ 可对角化。
  • $m(\lambda) = (\lambda-1)^2 \implies$ 存在一条长度为 2 的链 $\implies$ 不可对角化。

4. 全局视角：空间的彻底分解

既然单个 Jordan 块对应一条“链”（循环子空间），那么把视野拉远，整个线性空间 $V$ 变成了一幅怎样的图景？

这就是“空间分解”的终极形态： 线性变换 $\mathbf{A}$ 把空间 $V$ 拆解成了一个个互不干扰的“多米诺阵列”（不变子空间）。

$$ V = V_{\lambda_1} \oplus V_{\lambda_2} \oplus \dots \oplus V_{\lambda_k} $$

每个 $V_{\lambda_i}$ 是广义特征子空间。而在每个阵列内部，又排列着若干条独立的链条：

$$ V_{\lambda_i} = C_1 \oplus C_2 \oplus \dots \oplus C_{m_i} $$

• 对角化：满地都是独立的单张骨牌（1维子空间），清清爽爽。
• Jordan形：有些骨牌连成了长串，空间就是由这些长短不一的链条拼出来的。

Jordan 标准形，说白了就是帮我们找到这组“最佳视角”，看清每一条链的长度和位置。

✍️ 课后实战：侦探游戏

1. （概念辨析） 设 $\mathbf{A}$ 是 3 阶非零矩阵，且 $\mathbf{A}^2 = \mathbf{O}$。 请写出 $\mathbf{A}$ 的 Jordan 标准形。
   🔐 点击查看解析 / Click to Reveal

   【解】

   1. 特征值：因为 $\mathbf{A}^2 = \mathbf{O}$，所以特征值全为 0。
   2. Jordan 块大小： 最小多项式 $m(\lambda)$ 必须整除 $\lambda^2$（因为 $x^2$ 是零化多项式）。 同时 $\mathbf{A} \neq \mathbf{O}$，所以 $m(\lambda) \neq \lambda$。 故 $m(\lambda) = \lambda^2$。 这意味着最大的 Jordan 块是 $2$ 阶。
   3. 构造 $\mathbf{J}$： $\mathbf{A}$ 是 3 阶的。必须有一个 2 阶块。剩下一个只能是 1 阶块。 $$ \mathbf{J} = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} $$
2. （多项式反推） 给定 5 阶矩阵 $\mathbf{A}$。 已知 $( \mathbf{A} - 2\mathbf{E} )^3 ( \mathbf{A} + \mathbf{E} )^2 = \mathbf{O}$， 且 $( \mathbf{A} - 2\mathbf{E} )^2 ( \mathbf{A} + \mathbf{E} ) \neq \mathbf{O}$。 若 $\mathbf{A}$ 的特征多项式为 $f(\lambda) = (\lambda-2)^3 (\lambda+1)^2$。 请写出 $\mathbf{A}$ 的 Jordan 标准形 $\mathbf{J}$。
   🔐 点击查看解析 / Click to Reveal

   【解】 由特征多项式 $f(\lambda) = (\lambda-2)^3 (\lambda+1)^2$ 可知，矩阵 $\mathbf{A}$ 的特征值为 $\lambda_1 = 2$（代数重数 3）和 $\lambda_2 = -1$（代数重数 2）。

   设 $\mathbf{A}$ 的最小多项式为 $m(\lambda)$。 由已知条件 $( \mathbf{A} - 2\mathbf{E} )^3 ( \mathbf{A} + \mathbf{E} )^2 = \mathbf{O}$ 可知，$m(\lambda)$ 必须整除 $(\lambda-2)^3 (\lambda+1)^2$。 又由条件 $( \mathbf{A} - 2\mathbf{E} )^2 ( \mathbf{A} + \mathbf{E} ) \neq \mathbf{O}$ 可知，$m(\lambda)$ 不能整除 $(\lambda-2)^2 (\lambda+1)$。

   综合上述限制，且 $m(\lambda)$ 必须是 $f(\lambda)$ 的因子，可判定最小多项式为： $$ m(\lambda) = (\lambda-2)^3 (\lambda+1)^2 $$

   根据 Jordan 标准形理论，最小多项式中因子的次数对应于该特征值对应的最大 Jordan 块的阶数：

   1. 对于 $\lambda=2$，最大 Jordan 块为 3 阶。因代数重数为 3，故该特征值对应的 Jordan 块只有一个 $\mathbf{J}_3(2)$。
   2. 对于 $\lambda=-1$，最大 Jordan 块为 2 阶。因代数重数为 2，故该特征值对应的 Jordan 块只有一个 $\mathbf{J}_2(-1)$。

   综上所述，$\mathbf{A}$ 的 Jordan 标准形为： $$ \mathbf{J} = \begin{pmatrix} \mathbf{J}_3(2) & \mathbf{0} \\ \mathbf{0} & \mathbf{J}_2(-1) \end{pmatrix} = \begin{pmatrix} 2 & 1 & 0 & 0 & 0 \\ 0 & 2 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 0 & -1 \end{pmatrix} $$