◎ 直觉重构：空间的解剖引言
前两天我们沉浸在几何的直觉里，那感觉很美妙。但如果到了考场上，面对一道冷冰冰的“证明秩不等式”的题目，光有直觉是不够的。
你需要一把手术刀。
在代数的大厦里，这把手术刀叫做“分块矩阵初等变换”，江湖人称“打洞技巧”。
什么是分块矩阵？
简单说，就是用横线和竖线把大矩阵切成小块。
$$ \mathbf{M} = \left( \begin{array}{c|c} \mathbf{A} & \mathbf{B} \\ \hline \mathbf{C} & \mathbf{D} \end{array} \right) $$
为什么这么做？分而治之。当矩阵阶数很高时，直接处理很困难，但如果能把它切成我们熟悉的小块（比如单位阵、零阵），运算就会变得像 $2 \times 2$ 矩阵一样简单。
核心法则： 分块矩阵的加法、数乘和转置都很直观，唯独乘法需要注意 —— 必须满足“前列分法”等于“后行分法”，且子块之间要能相乘（即不可交换顺序）。
打洞原理：广义初等变换
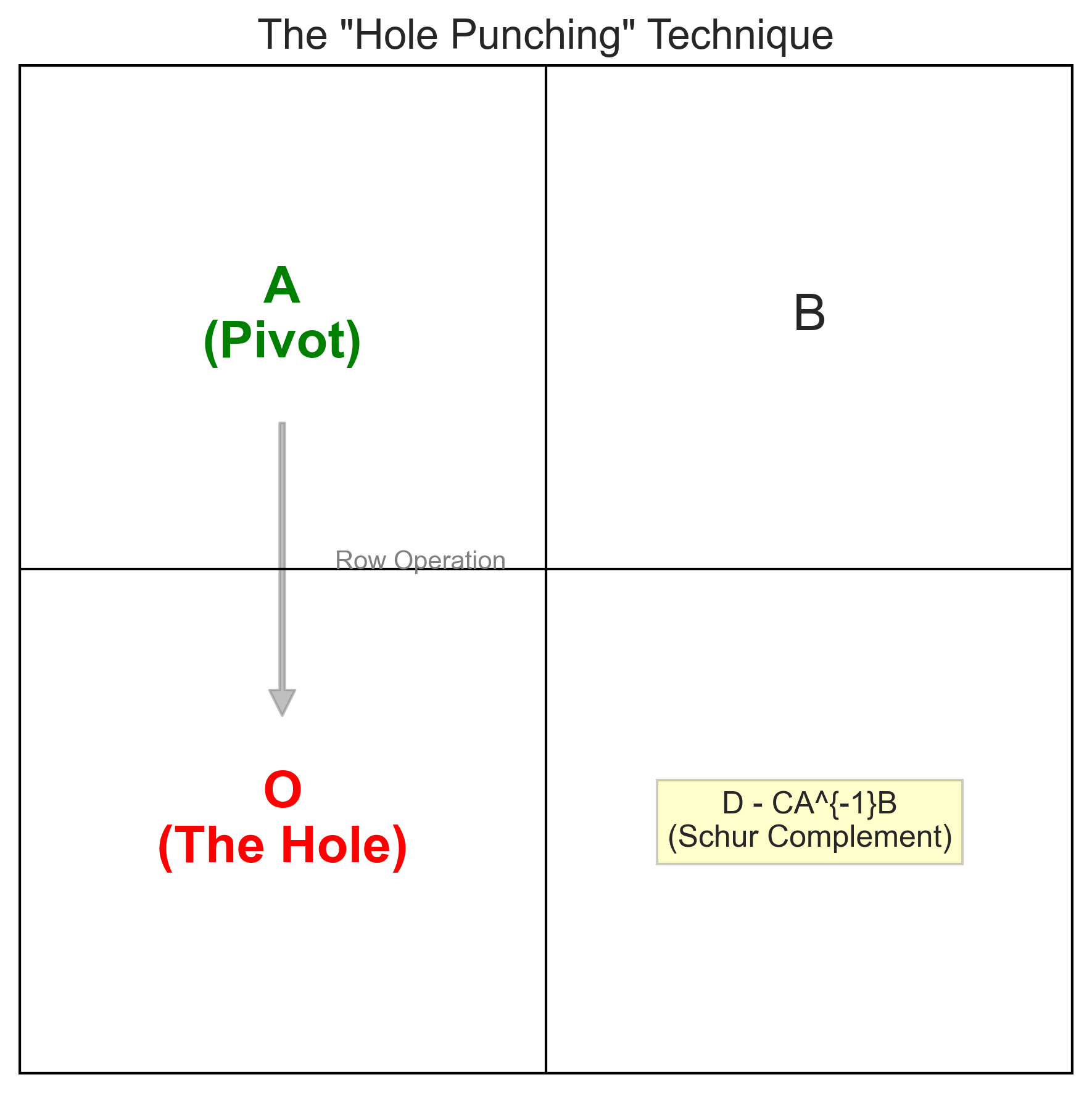◎ 打洞：将分块消为零块引子例题 设分块矩阵 $\mathbf{M} = \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{C} & \mathbf{D} \end{pmatrix}$，其中 $\mathbf{A}$ 是可逆方阵。
问题： 你能通过矩阵乘法，把 $\mathbf{C}$ 变成 $\mathbf{O}$ 吗？进而求出 $\mathbf{M}$ 的行列式吗？
【直觉破局】
回想一下高斯消元法。如果你想消去 $x$ 的系数，你会怎么做？你会用第二行减去第一行的 $k$ 倍。
在分块矩阵里，这叫做“广义初等行变换”。 我们要消去 $\mathbf{C}$，就得利用 $\mathbf{A}$。因为 $\mathbf{A}$ 可逆，我们可以构造“乘数” $\mathbf{C}\mathbf{A}^{-1}$。让第二行减去第一行左乘 $\mathbf{C}\mathbf{A}^{-1}$：
$$ \begin{pmatrix} \mathbf{E} & \mathbf{O} \\ -\mathbf{C}\mathbf{A}^{-1} & \mathbf{E} \end{pmatrix} \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{C} & \mathbf{D} \end{pmatrix} = \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{O} & \mathbf{D} - \mathbf{C}\mathbf{A}^{-1}\mathbf{B} \end{pmatrix} $$
看！$\mathbf{C}$ 位置变成了一个大大的 $\mathbf{O}$（洞）。 这时候，求行列式就简单了： $$ |\mathbf{M}| = |\mathbf{A}| \cdot |\mathbf{D} - \mathbf{C}\mathbf{A}^{-1}\mathbf{B}| $$ 右下角这一坨 $\mathbf{D} - \mathbf{C}\mathbf{A}^{-1}\mathbf{B}$，在数学上有个专门的名字：Schur 补 (Schur Complement)。
【核心结论】 分块初等变换不改变矩阵的秩。 这就好比拿着一把手术刀，把矩阵里复杂的杂质切除（变成 0），只留下最核心的骨架（对角块）。
核心重构：秩不等式的终极武器
几乎所有让人头秃的秩不等式（Sylvester, Frobenius），本质上都是在给分块矩阵“打洞”。
1. 核武器：构造分块矩阵证明不等式
定理 (Sylvester 不等式)：设 $\mathbf{A}_{m \times n}, \mathbf{B}_{n \times s}$，则 $r(\mathbf{AB}) \ge r(\mathbf{A}) + r(\mathbf{B}) - n$。
【证明】 构造分块矩阵 $\mathbf{M} = \begin{pmatrix} \mathbf{A} & \mathbf{O} \\ \mathbf{E}_n & \mathbf{B} \end{pmatrix}$。
第一步（打洞消元求秩）： 利用 $\mathbf{E}_n$ 将右边的 $\mathbf{B}$ 消去（$C_2 - C_1\mathbf{B}$）： $$ \begin{pmatrix} \mathbf{A} & \mathbf{O} \\ \mathbf{E}_n & \mathbf{B} \end{pmatrix} \xrightarrow{C_2 - C_1\mathbf{B}} \begin{pmatrix} \mathbf{A} & -\mathbf{AB} \\ \mathbf{E}_n & \mathbf{O} \end{pmatrix} \cong \begin{pmatrix} \mathbf{E}_n & \mathbf{O} \\ \mathbf{O} & \mathbf{AB} \end{pmatrix} $$ 故该分块矩阵的秩为：$r(\mathbf{M}) = n + r(\mathbf{AB})$。
第二步（利用性质放缩）： 对于下三角分块 $\begin{pmatrix} \mathbf{X} & \mathbf{O} \\ \mathbf{Y} & \mathbf{Z} \end{pmatrix}$，其秩 $\ge r(\mathbf{X}) + r(\mathbf{Z})$（因为 $\mathbf{X}$ 的行无关组和 $\mathbf{Z}$ 的行无关组“错开”了，互不干扰）。 所以，原矩阵的秩满足：$r(\mathbf{M}) \ge r(\mathbf{A}) + r(\mathbf{B})$。
综上：$n + r(\mathbf{AB}) \ge r(\mathbf{A}) + r(\mathbf{B})$，移项即得证。
定理 (Frobenius 不等式)：$r(\mathbf{ABC}) \ge r(\mathbf{AB}) + r(\mathbf{BC}) - r(\mathbf{B})$。
【证明】 构造 $\mathbf{M} = \begin{pmatrix} \mathbf{AB} & \mathbf{O} \\ \mathbf{B} & \mathbf{BC} \end{pmatrix}$。
- 消 $\mathbf{BC}$：$C_2 - C_1 \mathbf{C} \implies \begin{pmatrix} \mathbf{AB} & -\mathbf{ABC} \\ \mathbf{B} & \mathbf{O} \end{pmatrix}$。
- 消 $\mathbf{AB}$：$R_1 - \mathbf{A} R_2 \implies \begin{pmatrix} \mathbf{O} & -\mathbf{ABC} \\ \mathbf{B} & \mathbf{O} \end{pmatrix}$。 此时 $r(\mathbf{M}) = r(\mathbf{B}) + r(\mathbf{ABC})$。 另一方面，由分块性质，$r(\mathbf{M}) \ge r(\mathbf{AB}) + r(\mathbf{BC})$。 联立得证。
✍️ 课后实战：手术刀操作指南
- （基础实操） 设 $\mathbf{A}, \mathbf{D}$ 分别是 $m$ 阶和 $n$ 阶的可逆方阵，$\mathbf{B}$ 是 $m \times n$ 矩阵。 试利用分块矩阵的初等行变换（打洞），求分块矩阵 $\mathbf{M} = \begin{pmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{O} & \mathbf{D} \end{pmatrix}$ 的逆矩阵。
🔐 点击查看解析 / Click to Reveal
- （北大考研题） 设 $\mathbf{A}$ 是 $n$ 阶方阵且 $\mathbf{A}^2 = \mathbf{A}$（幂等矩阵）。 证明：$r(\mathbf{A}-\mathbf{E}) + r(\mathbf{A}) = n$。
🔐 点击查看解析 / Click to Reveal
- （必考推导） 伴随矩阵 $\mathbf{A}^*$ 的秩与原矩阵 $\mathbf{A}$ 的秩有何关系？请利用公式 $\mathbf{A}\mathbf{A}^* = |\mathbf{A}|\mathbf{E}$ 及本节证明的 Sylvester 不等式进行推导。
🔐 点击查看解析 / Click to Reveal
【解】 这是一个经典的“三态分布”结论：
- 情形 1：$r(\mathbf{A})=n$ $\mathbf{A}$ 可逆 $\implies |\mathbf{A}| \neq 0 \implies \mathbf{A}^*$ 也可逆 $\implies r(\mathbf{A}^*) = n$。
- 情形 2：$r(\mathbf{A})=n-1$ 此时 $|\mathbf{A}|=0$，代入公式得 $\mathbf{A}\mathbf{A}^* = \mathbf{O}$。 根据 Sylvester 不等式（$r(\mathbf{AB}) \ge r(\mathbf{A}) + r(\mathbf{B}) - n$），取 $\mathbf{B}=\mathbf{A}^*$： $$ 0 = r(\mathbf{O}) = r(\mathbf{A}\mathbf{A}^*) \ge r(\mathbf{A}) + r(\mathbf{A}^*) - n $$ 代入 $r(\mathbf{A}) = n-1$，得： $$ 0 \ge (n-1) + r(\mathbf{A}^*) - n \implies r(\mathbf{A}^*) \le 1 $$ 又因为 $r(\mathbf{A})=n-1$，说明 $\mathbf{A}$ 中至少存在一个非零子式，即 $\mathbf{A}^*$ 中至少有一个元素不为 0，所以 $r(\mathbf{A}^*) \ge 1$。 综上，$r(\mathbf{A}^*) = 1$。
- 情形 3：$r(\mathbf{A}) < n-1$ $\mathbf{A}$ 的所有 $n-1$ 阶子式全为 0。根据伴随矩阵定义，$\mathbf{A}^*$ 的所有元素（代数余子式）全为 0，即 $\mathbf{A}^* = \mathbf{O}$，所以 $r(\mathbf{A}^*) = 0$。
