◎ 图解：四个子空间的宏伟蓝图 —— 它们在输入与输出空间中两两正交，构成了完整的世界

引言

在 Day 1 中，我们将矩阵视为“运动”。今天，我们要把镜头拉远，看看这个运动发生的舞台。

对于任意 $m \times n$ 的矩阵 $\mathbf{A}$，它并不只是把一堆数字乘来乘去，它像一把精细的手术刀，将输入空间 $\mathbb{R}^n$ 和输出空间 $\mathbb{R}^m$ 切割成了四个界限分明的子空间 (Subspaces)。

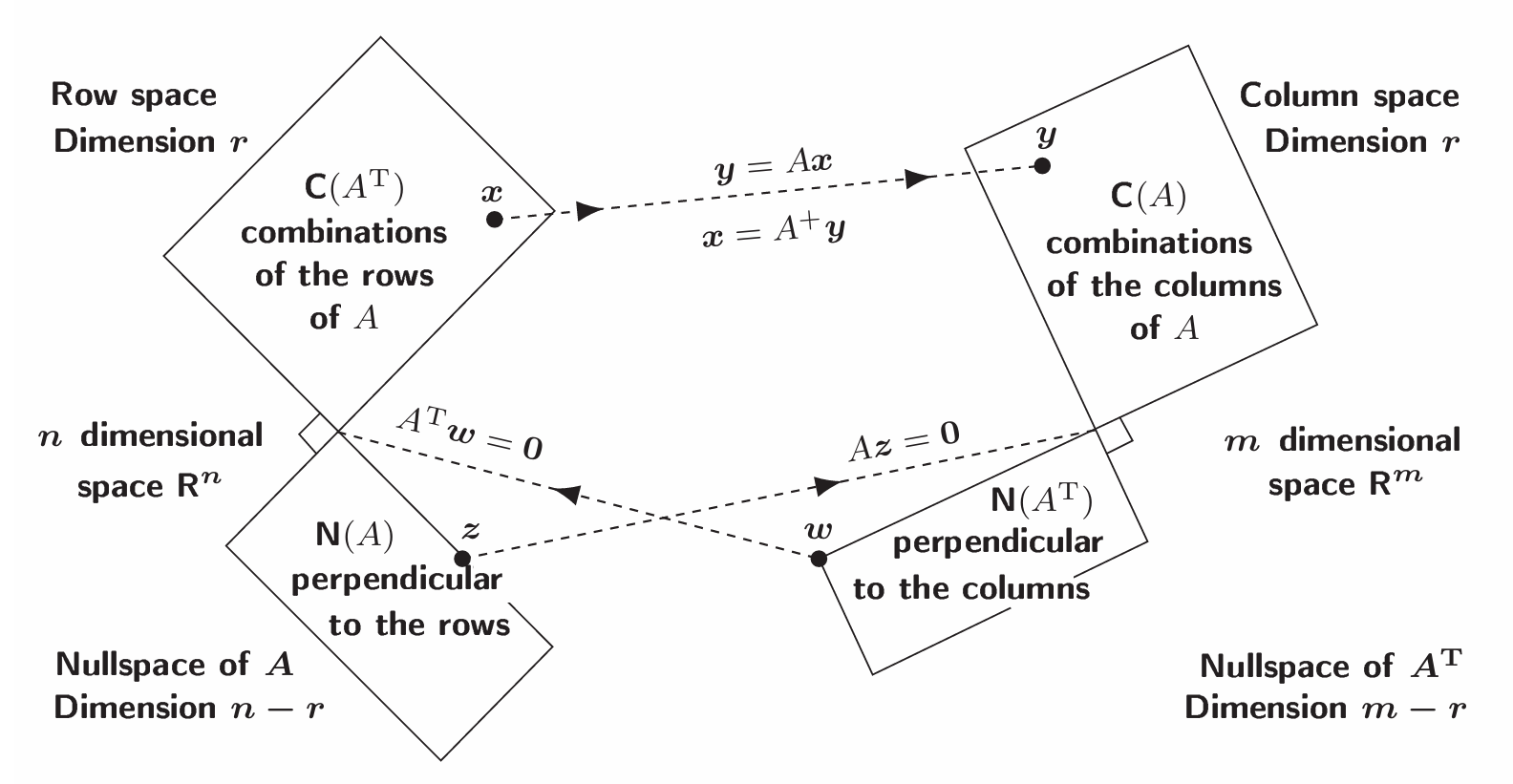◎ Strang 的“宇宙图景”：两个世界，四个空间

理解这四个子空间及其关系，被 Gilbert Strang 教授称为**“线性代数基本定理” (The Fundamental Theorem of Linear Algebra)**。它是你理解 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 解的结构、最小二乘法甚至 SVD 的地基。

1. 定义：舞台上的四个角色

在使用几何直觉之前，我们必须先用严格的数学语言界定它们。

输入空间 $\mathbb{R}^n$ 中的两个主角

1. 行空间 (Row Space, $\mathcal{R}(\mathbf{A}^\mathsf{T})$)： 由 $\mathbf{A}$ 的行向量生成的空间。它是所有行向量的线性组合。 $$\mathcal{R}(\mathbf{A}^\mathsf{T}) = { \mathbf{A}^\mathsf{T}\boldsymbol{y} \mid \boldsymbol{y} \in \mathbb{R}^m } \subset \mathbb{R}^n$$
2. 零空间 (Null Space, $\mathcal{N}(\mathbf{A})$)： 所有被矩阵“消灭”的向量。 $$\mathcal{N}(\mathbf{A}) = { \boldsymbol{x} \in \mathbb{R}^n \mid \mathbf{A}\boldsymbol{x} = \boldsymbol{0} } \subset \mathbb{R}^n$$

输出空间 $\mathbb{R}^m$ 中的两个主角

3. 列空间 (Column Space, $\mathcal{R}(\mathbf{A})$)： 由 $\mathbf{A}$ 的列向量生成的空间。也就是方程 $\mathbf{A}\boldsymbol{x}=\boldsymbol{b}$ 中所有可能有解的 $\boldsymbol{b}$。 $$\mathcal{R}(\mathbf{A}) = { \mathbf{A}\boldsymbol{x} \mid \boldsymbol{x} \in \mathbb{R}^n } \subset \mathbb{R}^m$$
4. 左零空间 (Left Null Space, $\mathcal{N}(\mathbf{A}^\mathsf{T})$)： 矩阵 $\mathbf{A}^\mathsf{T}$ 的零空间。之所以叫“左”，是因为 $\mathbf{A}^\mathsf{T}\boldsymbol{y} = \boldsymbol{0} \iff \boldsymbol{y}^\mathsf{T}\mathbf{A} = \boldsymbol{0}^\mathsf{T}$。 $$\mathcal{N}(\mathbf{A}^\mathsf{T}) = { \boldsymbol{y} \in \mathbb{R}^m \mid \mathbf{A}^\mathsf{T}\boldsymbol{y} = \boldsymbol{0} } \subset \mathbb{R}^m$$

2. 核心定理：正交与互补

这四个空间不是随意摆放的，它们之间存在着极强的正交 (Orthogonality) 约束。

定理 1：行空间 $\perp$ 零空间

结论：零空间中的每一个向量，都垂直于行空间中的每一个向量。 $$\mathcal{N}(\mathbf{A}) \perp \mathcal{R}(\mathbf{A}^\mathsf{T})$$

【证明】 设 $\boldsymbol{x} \in \mathcal{N}(\mathbf{A})$，即 $\mathbf{A}\boldsymbol{x} = \boldsymbol{0}$。 将 $\mathbf{A}\boldsymbol{x}$ 按行展开： $$ \begin{pmatrix} - & \boldsymbol{r}_1^\mathsf{T} & - \\ \vdots & \vdots & \vdots \\ - & \boldsymbol{r}_m^\mathsf{T} & - \end{pmatrix} \boldsymbol{x} = \begin{pmatrix} \boldsymbol{r}_1^\mathsf{T} \boldsymbol{x} \\ \vdots \\ \boldsymbol{r}_m^\mathsf{T} \boldsymbol{x} \end{pmatrix} = \begin{pmatrix} 0 \\ \vdots \\ 0 \end{pmatrix} $$ 这说明 $\boldsymbol{x}$ 与 $\mathbf{A}$ 的每一行 $\boldsymbol{r}_i$ 都垂直（内积为 0）。 既然 $\boldsymbol{x}$ 垂直于所有基向量，它自然垂直于这些基向量生成的整个行空间。

定理 2：维数守恒 (Rank-Nullity Theorem)

输入空间 $\mathbb{R}^n$ 被完美地分割了。 $$n = \dim(\mathcal{R}(\mathbf{A}^\mathsf{T})) + \dim(\mathcal{N}(\mathbf{A})) = r + (n-r)$$ 这意味着：零空间是行空间的正交补 (Orthogonal Complement)。 $$\mathcal{N}(\mathbf{A}) = (\mathcal{R}(\mathbf{A}^\mathsf{T}))^\perp$$

同理，输出空间 $\mathbb{R}^m$ 也被分割为： $$m = r + (m-r)$$ 即列空间与左零空间正交互补：$\mathcal{R}(\mathbf{A}) \perp \mathcal{N}(\mathbf{A}^\mathsf{T})$。

3. 深度解析：解的几何结构

理解了正交性，我们就能看透线性方程组 $\mathbf{A}\boldsymbol{x} = \boldsymbol{b}$ 的本质。

通解的公式我们都会背：$\boldsymbol{x} = \boldsymbol{x}^* + k\boldsymbol{\eta}$。 但在几何上，这不仅是“特解+齐次解”，而是**“行空间分量 + 零空间分量”**。

任意向量 $\boldsymbol{x} \in \mathbb{R}^n$ 都可以唯一分解为： $$\boldsymbol{x} = \boldsymbol{x}_r + \boldsymbol{x}_n$$ 其中 $\boldsymbol{x}_r \in \mathcal{R}(\mathbf{A}^\mathsf{T})$，$\boldsymbol{x}_n \in \mathcal{N}(\mathbf{A})$。

当 $\mathbf{A}$ 作用于 $\boldsymbol{x}$ 时： $$\mathbf{A}\boldsymbol{x} = \mathbf{A}(\boldsymbol{x}_r + \boldsymbol{x}_n) = \mathbf{A}\boldsymbol{x}_r + \mathbf{A}\boldsymbol{x}_n = \mathbf{A}\boldsymbol{x}_r + \boldsymbol{0} = \boldsymbol{b}$$

直觉炸裂：

1. 一一映射：矩阵 $\mathbf{A}$ 实际上构建了一个从行空间到列空间的一对一可逆映射（双射）。
2. 无效信息：零空间分量 $\boldsymbol{x}_n$ 是被矩阵“吃掉”的无效信息。
3. 最佳解：如果方程有无穷多解，哪一个最好？通常我们选长度最短的那个。由于 $\boldsymbol{x}_r \perp \boldsymbol{x}_n$，由勾股定理： $$|\boldsymbol{x}|^2 = |\boldsymbol{x}_r|^2 + |\boldsymbol{x}_n|^2$$ 显然，当 $\boldsymbol{x}_n = \boldsymbol{0}$ 时，$\boldsymbol{x}$ 的长度最小。

   结论：行空间中的那个解 $\boldsymbol{x}_r$，就是方程的最小范数解。

✍️ 课后实战

习题 1：画出子空间 给定矩阵 $\mathbf{A} = \begin{pmatrix} 1 & 2 \\ 3 & 6 \end{pmatrix}$。

1. 求出四个子空间的基底。
2. 在二维平面上画出输入空间 $\mathbb{R}^2$ 中的行空间和零空间，验证它们的正交性。

🔐 点击查看解析 / Click to Reveal

【解】

1. 行空间：由第一行 $(1, 2)$ 生成（第二行是第一行的3倍，冗余）。基底为 $\begin{pmatrix} 1 \\ 2 \end{pmatrix}$。
2. 零空间：解 $x_1 + 2x_2 = 0$。令 $x_2 = 1 \implies x_1 = -2$。基底为 $\begin{pmatrix} -2 \\ 1 \end{pmatrix}$。
3. 列空间：由第一列 $(1, 3)^\mathsf{T}$ 生成。基底为 $\begin{pmatrix} 1 \\ 3 \end{pmatrix}$。
4. 左零空间：$\mathbf{A}^\mathsf{T} = \begin{pmatrix} 1 & 3 \\ 2 & 6 \end{pmatrix}$。解 $y_1 + 3y_2 = 0$。基底为 $\begin{pmatrix} -3 \\ 1 \end{pmatrix}$。

几何验证： 输入空间中，行空间是直线 $y=2x$ 的方向（向量 $(1,2)$），零空间是向量 $(-2, 1)$。 点积：$1 \cdot (-2) + 2 \cdot 1 = 0$。它们确实垂直！

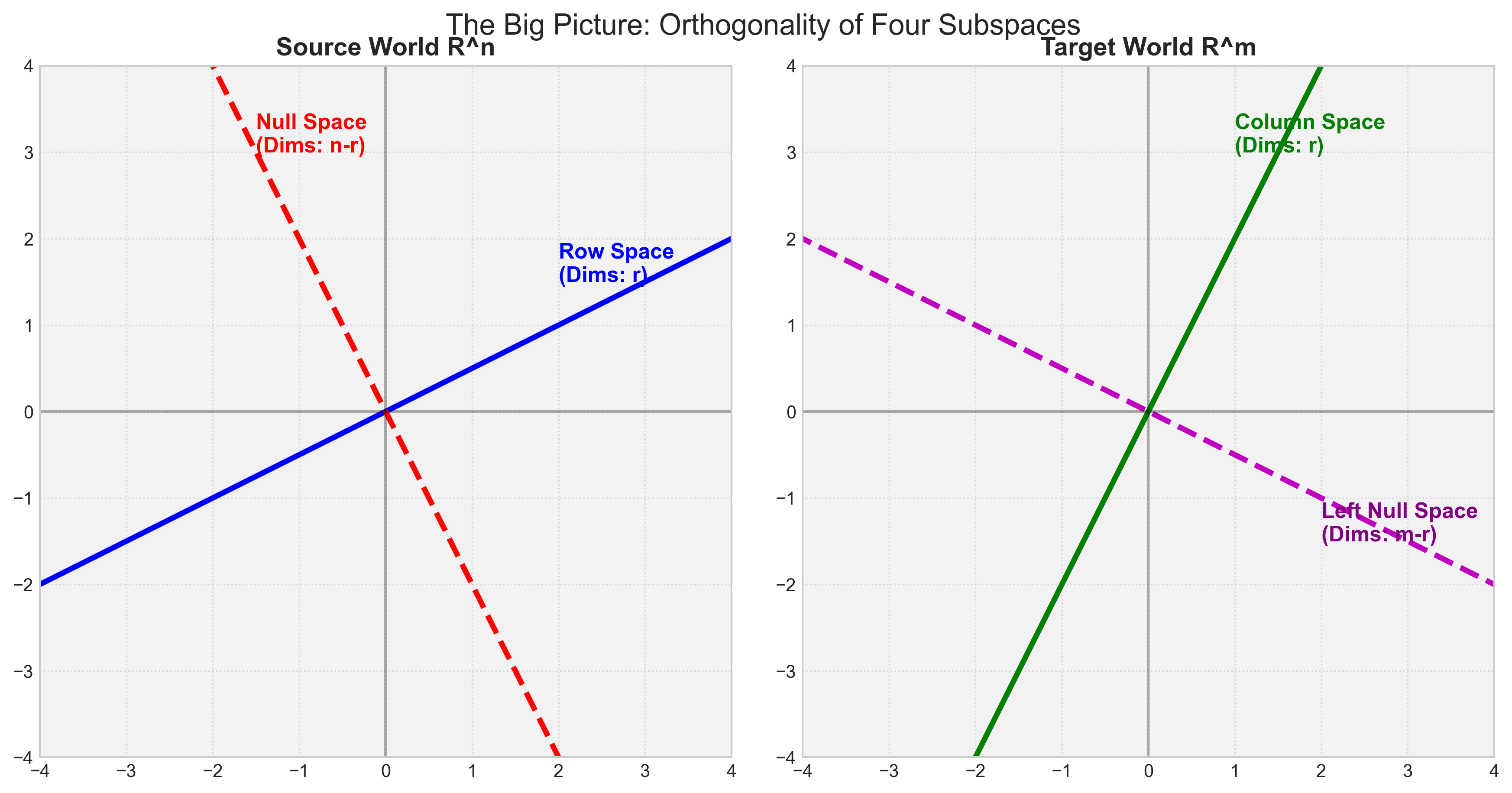◎ 直觉验证：两个世界的垂直十字架

习题 2：证明最小范数解（伪逆原理） 设方程 $\mathbf{A}\boldsymbol{x} = \boldsymbol{b}$ 有解。证明：在所有的解中，唯一存在一个 $\boldsymbol{x} \in \mathcal{R}(\mathbf{A}^\mathsf{T})$，且该解的范数（长度）最小。

线性代数重构计划 (The Plan)

• Day 0: 为什么你算对了所有的题，却依然不懂线性代数？
• Day 1: 别把矩阵当数字表 —— 线性变换与数据压缩
• Day 2: 空间的解剖学 —— 四大子空间与正交性
• Day 3: 信息的维度 —— 秩、分块与“打洞”绝技
• Day 4: 算子的灵魂 —— 特征值、几何重数与对角化
• Day 5: 无法对角化的妥协 —— Jordan 标准形与最简结构
• Day 6: 缠绕的算子 —— 可交换矩阵与不变子空间
• Day 7: 矩阵的基因 —— 奇异值分解 (SVD)